

Podemos recordar fácilmente el valor de las razones trigonométricas seno y coseno de los ángulos básicos si los escribimos de esta forma:
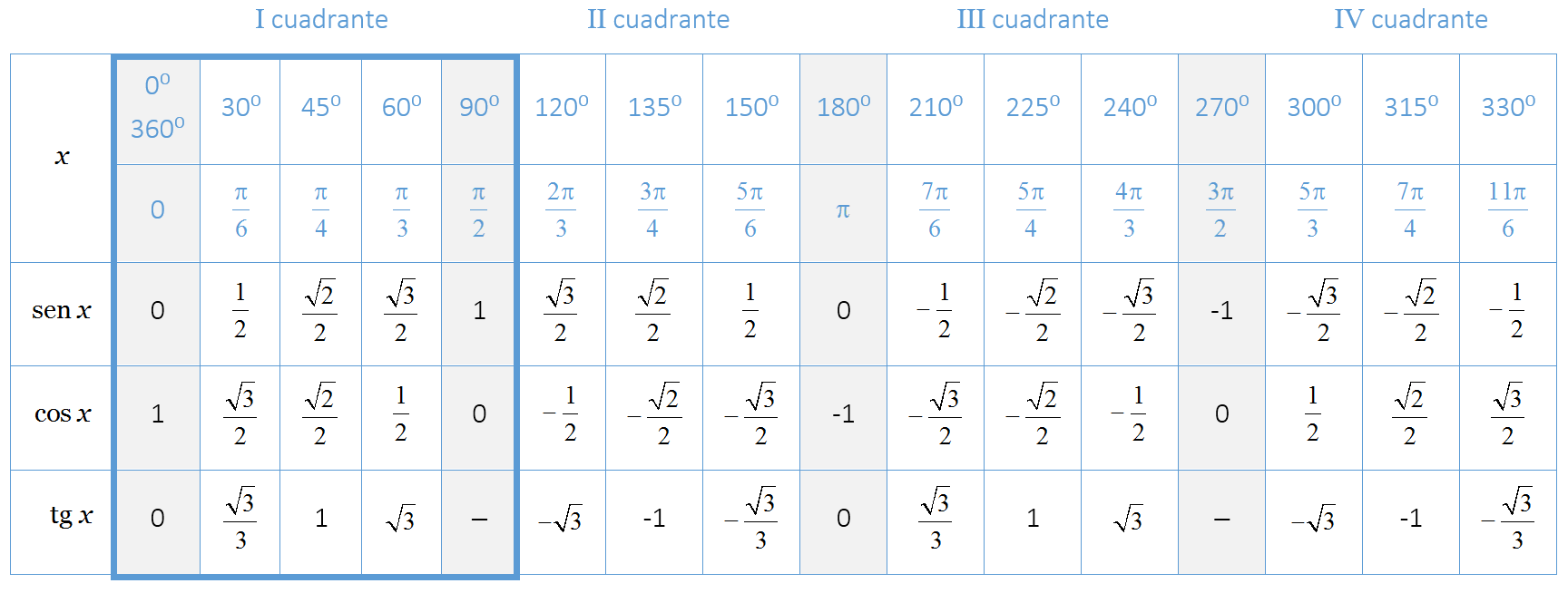
En la siguiente tabla se dan los valores del seno, coseno y tangente para los principales ángulos medidos en grados `[0º,360º]` y en radianes `[0,2pi]`. Para otros ángulos se utilizará la calculadora.
[ Trigonometría ]
Problema r003
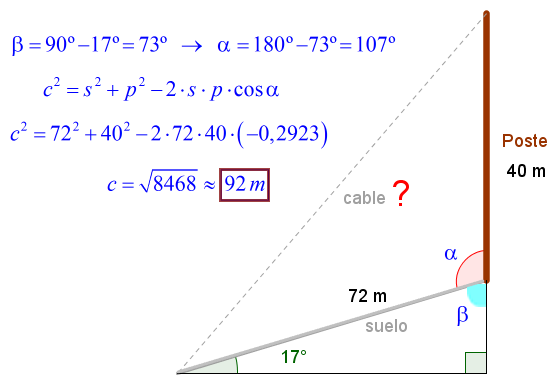
Un poste vertical de 40 m de altura está en una cuesta que forma un ángulo de 17º con la horizontal. Calcula la longitud mínima de cable que llegará de la parte superior del poste a un punto a 72 m cuesta abajo (medido desde la base del poste).
Hoy ........ 2345
Ayer ....... 1916
Mes ....... 22128
TOTAL ... 6468662
Hay 36 invitados y ningún miembro en línea