
La Teoría Combinatoria resuelve los problemas que aparecen al estudiar y cuantificar las diferentes formas de agrupar los elementos de un conjunto. Una de éstas maneras son las variaciones.
─ Número de variaciones ordinarias: `V_m^n = m (m-1) (m-2) ... (m-n+1)`
─ Número de variaciones con repetición: `VR_m^n = m^n`
Se llaman variaciones ordinarias, o variaciones sin repetición, de m elementos, tomados de n en n, a los diferentes grupos que con ellos se pueden formar, de tal modo que en cada grupo entren n elementos distinos y que un grupo se diferencia de los demás bien en alguno de los elementos o bien en el orden de colocación de dichos elementos.
Se llaman variaciones con repetición, de m elementos, tomados de n en n, a los diferentes grupos que con ellos se pueden formar, de tal modo que en cada grupo entren n elementos, pudiendo alguno repetirse una o varias veces y considerando dos grupos distintos si se diferencian en algún elemento o en el orden en que están colocados.
[ Combinatoria ]
Problema r011
Hallar el valor de la derivada de `f(x)=5x-x^2` en el punto x=3, por la definición.
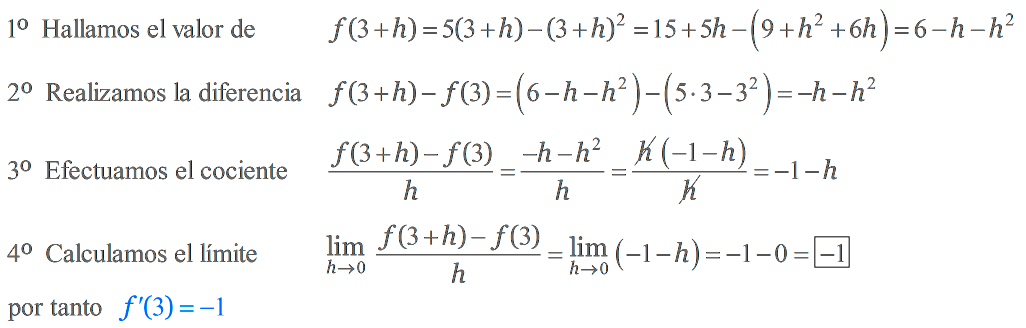
Hoy ........ 662
Ayer ....... 1798
Mes ....... 46952
TOTAL ... 5614504
Hay 28 invitados y ningún miembro en línea