
La función `f` es derivable en el punto `c`
Si `Lim_{h->0} {f(c+h)-f(c)}/h` existe
Este límite se designa por `f'(c)` y se denomina derivada de `f` en el punto `c`.
También decimos que `f` es derivable si `f` es derivable en `c` para todo `c` del dominio de `f`.
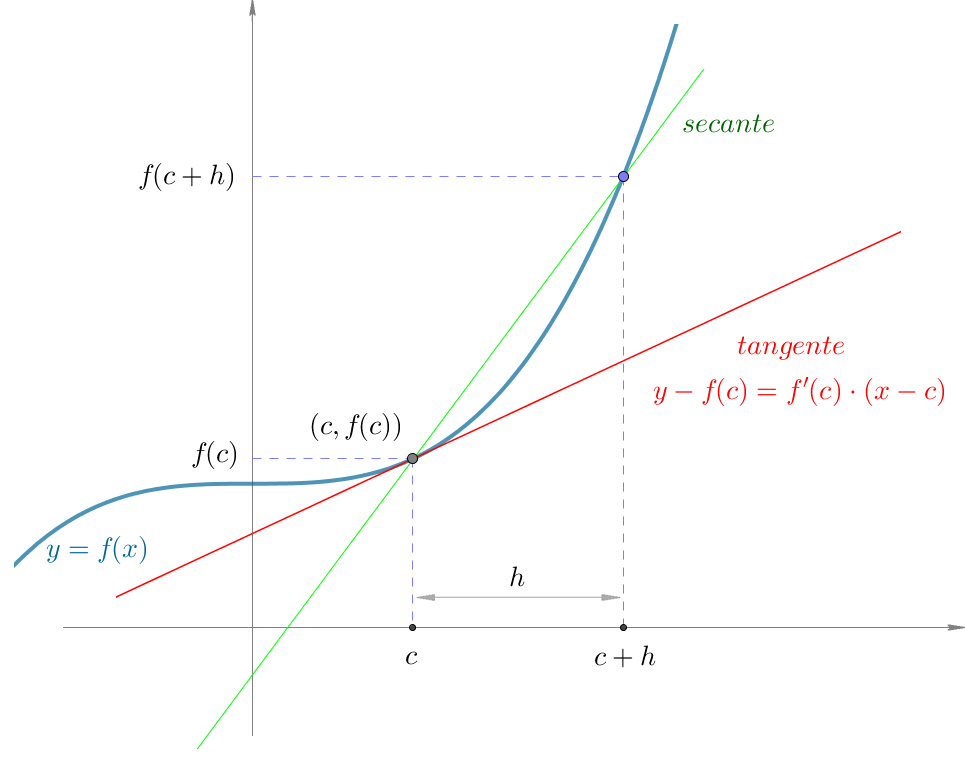
Se llama Función Derivada (o sencillamente derivada) a la función `f'` que asigna a cada valor de `x` la derivada de `f` en ese punto, es decir, la pendiente de la curva `y=f(x)` en ese punto.
`f'(x)=Lim_{h->0} {f(x+h)-f(x)}/h`
La derivada `f'(x)` nos proporciona una fórmula para calcular la pendiente de la recta tangente a la gráfica de `f` en el punto `(x,f(x))`
También se utiliza `d/dx f(x)` para designar a la función derivada. (Notación debida al matemático alemán Leibniz).
Una función derivable es continua, pero una función continua no necesariamente es derivable. Estos son algunos ejemplos de funciones continuas no derivables por tener derivadas laterales distintas (1,3 y 4) o tangentes verticales (2):

[ Cálculo ]
Problema r008
Calcular las coordenadas de los puntos que dividen al segmento de origen A(-5,-2) y extremo B(7,2) en tres partes iguales.

Hoy ........ 848
Ayer ....... 3272
Mes ....... 46874
TOTAL ... 6350314
Hay 40 invitados y ningún miembro en línea